Formula for Maximum Number of Segments Determined by N Points
Max_cuts nn n 22 SO for eg. Find the maximum and minimum value of the function.
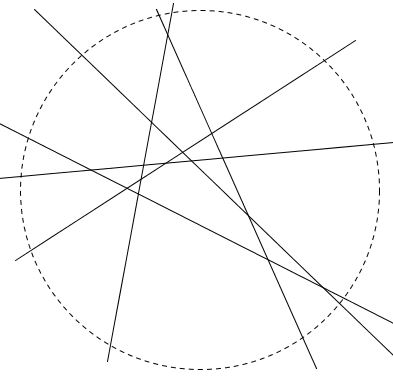
Number Of Regions N Lines Divide Plane
Fx 2x 3 - 3x 2 - 12 x 5.
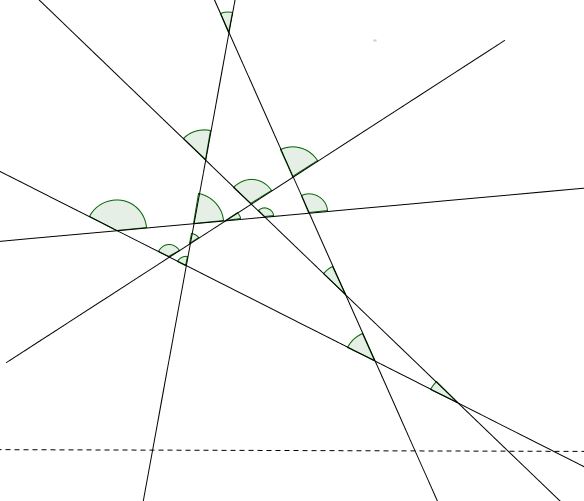
. Given an array a1 with size n1 and two integers A and B are given. Because no three of the points are nonlinear any two of them will serve as the endpoints of a line segment. I included a diagram below to show what lines are added with a 6th point.
So 2 can also be assigned to the first segment but it will. F-1 2-1 3 - 3-1 2 - 12-1 5 2-1 - 31 12 5 -2 - 3 12 5 -5 17 12. Displaystyle F n choose 4 n choose 22 The fifth column of Bernoullis triangle k 4 gives the maximum number of regions in the problem of dividing a circle into areas for n 1 points where n 4.
This problem can be thought of as a number of ways to select any two lines among n line. If n2 max_cuts4 22 2 22 4 similarily if n3 max_cuts7. Place the scale on the piece of paper and.
5 points on a line 10 segments. The basic idea of this approach is that you choose the highest number of segments such that none of the segments are small less than 5 of the sample. Level up your coding skills and quickly land a job.
We could use this logic to write a formula for finding the number of diagonals determined by a circle with n points. Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site. Answer 1 of 4.
Input N8 a3 b1 c2. 0 5 and 4 9 The point 1 can be assigned to the first segment 0 5 No points can be assigned to the second segment. Therefore maximum point -1 12 minimum point 2 15 Example 2.
Critical Thinking Explain how rescue teams could use two of the postulates from this lesson to locate a distress signal. For example 2 points on a line 1 line segment. The number of chords forming the outside of the polygon is the same as the number of points since there would be one chord connecting each point to the next as we move around the perimeter of the circle.
Given the task is to find the maximum of segments that can contain the given points. This rule has two justifications. If there are n points then the maximum number of lines possible is nn-12 and that maximum is attained of no three points are collinear.
The random condition is to say that the points must be placed to get the maximum number of regions. I hope it helps you see things. Given the task is to find the maximum number of line segments of lengths a b and c that can be formed from given positive integer N.
You can apply following formula to get maximum numbers of pieces with n cuts on a flat circular surface. This formula would be. From the given array a1 n1 line segments can be formed with starting and ending points as a1 i.
F-1 -18 0 Maximum. The maximum number of regions that we can obtain from crossing chords with 6 points is 31. The powers of 2 pattern breaks down when we choose 6 points on a circle.
A 4 a 6 will intersect a 1 a 5 a 2 a 5 and a 3 a 5. 3 points on a line 3 segments. Lets now understand what we have to do using an example.
X 3 - 3x 2 - 9x 12. If we add a 7th point and count very carefully we get 57 regions. Write a formula for the maximum number of segments determined by n points.
Draw a line segment of a given length 6 rm cm. Write a formula for the maximum number of segments determined by n points. A 4 a 6 is similar to a 2 a 6.
Explanation N can be divided into 8 segments of b which is maximum number of segments that can be made. So the total number of points nC2. A nice 2 n-1 pattern we say where n is the number of points on the circle.
1 on a question. The picture above right gives the answer 31 regions for n6 not 32 but 31. For the cases when n is.
After that the counting becomes tricky and we wonder what the general relationship might be. Line Segments are 1-X 1Y 5-X 5Y ie. F n 4 n 2 2.
As every line intersects with others that are selected. Manager at Capgemini India 2017-present Answered 3 years ago Author has 222 answers and 3647K answer views. And then our hopes are quickly dashed when we look at the case of 6 points.
Take a scale and look for the zero marking which is the beginning of the scale. To find the maximum value substitute x -1 in fx. The steps to draw a line segment are as follows.
It seems that there is O N3log N algorithm iterate through all pairs of points - O N2 for each point of the rest compute radius of circle including that point and the selected pair of points - O N sort points by this radius - O Nlog N select from the resulting array the biggest group with same radius - O N Actually given two points and radius two circles are. The answer is displaystyle nchoose 3nchoose 2nchoose 1nchoose 0 As weve seen the solution employs the 1-1 correspondence between the regions that have the lowest vertex and the set of all points of intersection of the given lines by assigning to each such region its lowest extreme vertex. 6 choose 2 or C 62 6 24 6x52 15.
Write a general rule of formula for finding the number of segments that can be named by a given number of points on a line. This is the best place to expand your knowledge and get prepared for your next interview. The no small segments and extent of association with other data methods are both closely related to strategic usefulness.
Thus the maximum number of additional regions moving from n 5 points to n 6 points is 23433 or 15. Below is the implementation of the above approach.

Maximum Number That Can Be Display On Seven Segment Display Using N Segments Geeksforgeeks

Number Of Regions N Lines Divide Plane
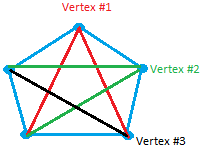
Number Of Segments Between Points
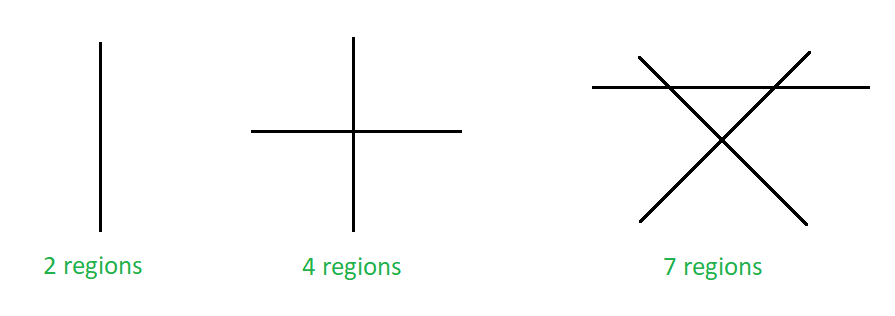
Maximum Number Of Region In Which N Non Parallel Lines Can Divide A Plane Geeksforgeeks
No comments for "Formula for Maximum Number of Segments Determined by N Points"
Post a Comment